Experimenter

There are several common scenarios encountered when experimenting with MOEAs:

1. Testing a new algorithm against many test problems
2. Comparing the performance of many algorithms across one or more problems
3. Testing the effects of different parameters

Platypus provides the experimenter module with convenient routines for performing these kinds of experiments. Furthermore, the experimenter methods all support parallelization.

Basic Use

Suppose we want to compare NSGA-II and NSGA-III on the DTLZ2 problem. In general, you will want to run each algorithm several times on the problem with different random number generator seeds. Instead of having to write many for loops to run each algorithm for every seed, we can use the experiment function. The experiment function accepts a list of algorithms, a list of problems, and several other arguments that configure the experiment, such as the number of seeds and number of function evaluations. It then evaluates every algorithm against every problem and returns the data in a JSON-like dictionary.

Afterwards, we can use the calculate function to calculate one or more performance indicators for the results. The result is another JSON-like dictionary storing the numeric indicator values. We finish by pretty printing the results using display.

from platypus import NSGAII, NSGAIII, DTLZ2, Hypervolume, experiment, calculate, display

if __name__ == "__main__":
    algorithms = [NSGAII, (NSGAIII, {"divisions_outer":12})]
    problems = [DTLZ2(3)]

    # run the experiment
    results = experiment(algorithms, problems, nfe=10000, seeds=10)

    # calculate the hypervolume indicator
    hyp = Hypervolume(minimum=[0, 0, 0], maximum=[1, 1, 1])
    hyp_result = calculate(results, hyp)
    display(hyp_result, ndigits=3)

The output of which appears similar to:

NSGAII
    DTLZ2
        Hypervolume : [0.361, 0.369, 0.372, 0.376, 0.376, 0.388, 0.378, 0.371, 0.363, 0.364]
NSGAIII
    DTLZ2
        Hypervolume : [0.407, 0.41, 0.407, 0.405, 0.405, 0.398, 0.404, 0.406, 0.408, 0.401]

Once this data is collected, we can then use statistical tests to determine if there is any statistical difference between the results. In this case, we may want to use the Mann-Whitney U test from scipy.stats.mannwhitneyu.

Note how we listed the algorithms: [NSGAII, (NSGAIII, {"divisions_outer":12})]. Normally you just need to provide the algorithm type, but if you want to customize the algorithm, you can also provide optional arguments. To do so, you need to pass a tuple with the values (type, dict), where dict is a dictionary containing the arguments. If you want to test the same algorithm with different parameters, pass in a three-element tuple containing (type, dict, name). The name element provides a custom name for the algorithm that will appear in the output. For example, we could use (NSGAIII, {"divisions_outer":24}, "NSGAIII_24"). The names must be unique.

Parallelization

One of the major advantages to using the experimenter is that it supports parallelization. In Python, there are several standards for running parallel jobs, such as the map function. Platypus abstracts these different standards using the Evaluator class. The default evaluator is the MapEvaluator, but parallel versions such as MultiprocessingEvaluator for Python 2 and ProcessPoolEvaluator for Python 3.

When using these evaluators, one must also follow any requirements of the underlying library. For example, MultiprocessingEvaluator uses the multiprocessing module available on Python 2, which requires the users to invoke freeze_support() first.

from platypus import *

if __name__ == "__main__":
    algorithms = [NSGAII, (NSGAIII, {"divisions_outer":12})]
    problems = [DTLZ2(3)]

    with ProcessPoolEvaluator(4) as evaluator:
        results = experiment(algorithms, problems, nfe=10000, evaluator=evaluator)

        hyp = Hypervolume(minimum=[0, 0, 0], maximum=[1, 1, 1])
        hyp_result = calculate(results, hyp, evaluator=evaluator)
        display(hyp_result, ndigits=3)

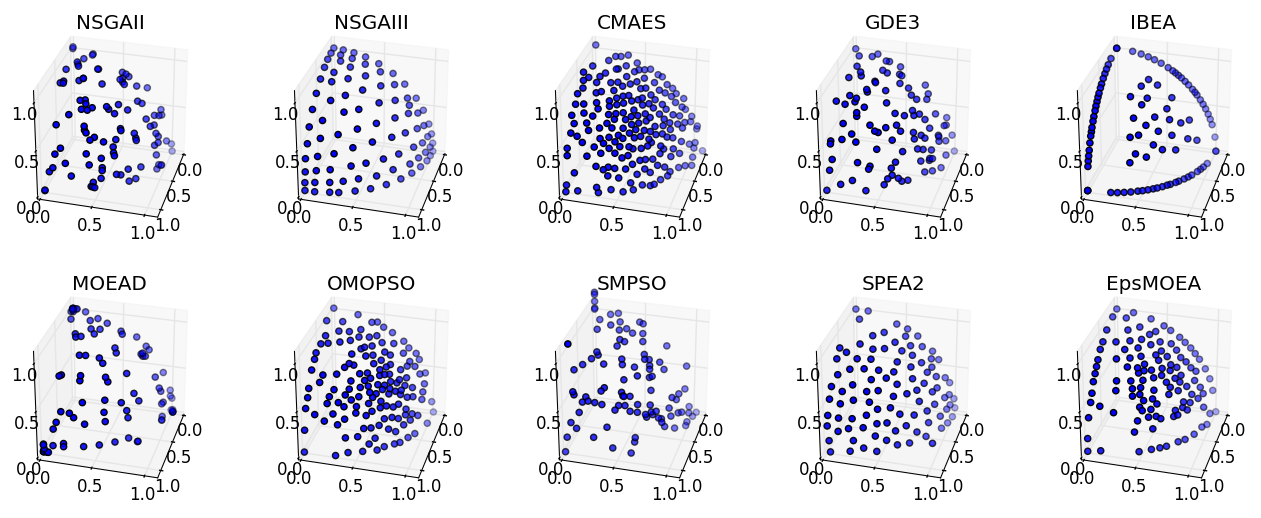
Comparing Algorithms Visually

Extending the previous examples, we can perform a full comparison of all supported algorithms on the DTLZ2 problem and display the results visually. Note that several algorithms, such as NSGA-III, CMAES, OMOPSO, and EpsMOEA, require additional parameters.

from platypus import *
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

if __name__ == '__main__':
    # setup the experiment
    problem = DTLZ2(3)

    algorithms = [NSGAII,
                  (NSGAIII, {"divisions_outer":12}),
                  (CMAES, {"epsilons":[0.05]}),
                  GDE3,
                  IBEA,
                  (MOEAD, {"weight_generator":normal_boundary_weights, "divisions_outer":12}),
                  (OMOPSO, {"epsilons":[0.05]}),
                  SMPSO,
                  SPEA2,
                  (EpsMOEA, {"epsilons":[0.05]})]

    # run the experiment using Python 3's concurrent futures for parallel evaluation
    with ProcessPoolEvaluator() as evaluator:
        results = experiment(algorithms, problem, seeds=1, nfe=10000, evaluator=evaluator)

    # display the results
    fig = plt.figure()

    for i, algorithm in enumerate(results.keys()):
        result = results[algorithm]["DTLZ2"][0]

        ax = fig.add_subplot(2, 5, i+1, projection='3d')
        ax.scatter([s.objectives[0] for s in result],
                   [s.objectives[1] for s in result],
                   [s.objectives[2] for s in result])
        ax.set_title(algorithm)
        ax.set_xlim([0, 1.1])
        ax.set_ylim([0, 1.1])
        ax.set_zlim([0, 1.1])
        ax.view_init(elev=30.0, azim=15.0)
        ax.locator_params(nbins=4)

    plt.show()

Running this script produces the figure below: